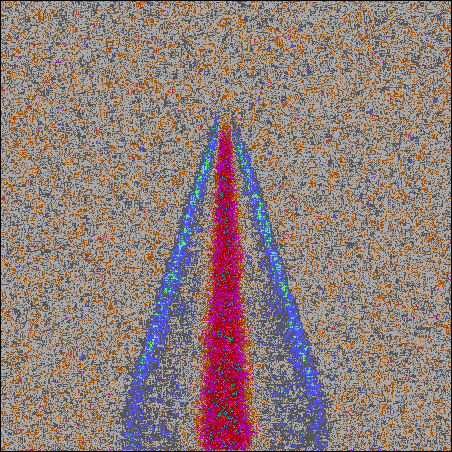Conference Record of the 1998 IEEE International Symposium
on Electrical Insulation, 7-10 June 1998, Washington, DC, USA.
Vol. 2., pp. 611--614.
Simulations of Gas-dynamic Flows During
Streamers Propagation at Liquid Dielectrics Breakdowns
A. L. Kupershtokh, D. A. Medvedev
Lavrentyev Institute of Hydrodynamics SB RAS
Novosibirsk, 630090, RUSSIA
Abstract
For the case of selfsimilar solution for the problem of streamer
channel expansion at the electric breakdown in liquid,
computations using the lattice gas (LG) and lattice Boltzmann
equation (LBE) methods were carried out. In the latter case, the
computation results agree well with theoretical calculations.
Computations of the prebreakdown stage of the propagation of a
rectilinear streamer channel were also carried out. Expansion of
the conductive channel and formation of compression waves
propagating with a speed close to the sound velocity in a
dielectric liquid were observed.
The stochastic evolution of the streamer structure was computed
with allowance for the gas-dynamic flows. In this case, the growth
proceeds due to both the hydrodynamic movement of the conductive
phase and the breakdown of new portions of the substance.
Transition between two mechanisms of development of the conductive
structure was demonstrated.
Introduction
An electric breakdown of dielectric liquids is known to occur by
propagation of a system of streamers (thin plasma channels) from
one electrode to another. A large body of experimental data points
to the important role of stochastic processes at breakdown of
solid and liquid dielectrics. One can cite as an example the
statistical lag time after the voltage supply to the gap, the
dissymmetry of the streamer system and the irreproducibility of
its detailed structure, the indented shape of oscillograms of the
prebreakdown current and the luminescence of the growing
structure, etc. Certain success has been recently achieved in the
modeling of these stochastic effects [1-4].
On the other hand, gas-dynamic flows (flows of compressible
liquid) of the surrounding dielectric have drawn little attention
so far. However, the formation of compression waves during the
streamer propagation and the expansion of streamer channels have
been already observed in the first experiments where the
high-speed photorecording of the breakdown process has been
conducted. Many experimental results point to the important role
of these processes not only at the channel stage, but also at the
prebreakdown stage of the streamer channel propagation. For
instance, data have been obtained [5] which clearly
indicate expansion and pulsations of streamer channels. At the
propagation stage, divergent shock waves with an approximately
conic shape have been observed.
Some experiments point to the decisive role of liquid flows
(including vortical ones) as the viscosity of dielectric liquids
increases. In this case, the fine structure of streamers vanishes
and their evolution resembles the expansion and growth of a cavity
(bubble) of irregular shape [6]. Similar processes have
been observed in certain development regimes of partial breakdown
[7].
However, so far there are no model that would allow one to
describe the entire complex of experimentally observed phenomena.
Lattice Gas methods
The lattice gas (LG) method [8] treats a liquid flow as the
dynamics of special particles which can move along the links of a
fixed lattice and suffer collisions and scattering in nodes. The
LG method is in a sense an extremely simplified method of
molecular dynamics.
An eight-directional LG model with three velocity levels 0, 1 and
$\sqrt{2}$ was used [9]. It allows one to describe the
energy release at the streamer tip.
Another modification of this method is the method of immiscible
lattice gases (ILG). Here two kinds (colors) of particles exist,
one for a dielectric liquid and the second for a conductive phase.
Collision rules are chosen to maximize the flux of particles of
given color to adjacent nodes with the majority of particles of
the same color. This gives rise to surface tension on the
interface.
Method "Lattice Boltzmann Equation"
This method has evolved from the lattice gas method. In this case
there is also a regular spatial lattice and a few velocity values
are possible at each node. The ensemble-averaged local
one-particle distribution functions are taken as variables. The
averaging leads to complete elimination of the statistical noise.
It allows one to considerably decrease the number of grid points
in the computation domain. This is possible, however, only at the
cost of giving up integer arithmetics. The LBE method can be
viewed as a solution of the kinetic equation for model particles.
The evolution equations are formally the same as for the lattice
gas. The collision operator, however, can be of any form. It
allows one to provide, for instance, Galilean invariance.
Moreover, the LBE method can be easily extended to three
dimensions. Presently, the collision operator in the BGK form
[10] is widely used. It simply means the relaxation to the
local equilibrium configuration which is determined by the
density, velocity, and temperature at a node. In the computations
we used a two-dimensional model with four velocity levels: 0, 1,
$\sqrt{2}$ and 2 (13 possible velocity vectors) [11].
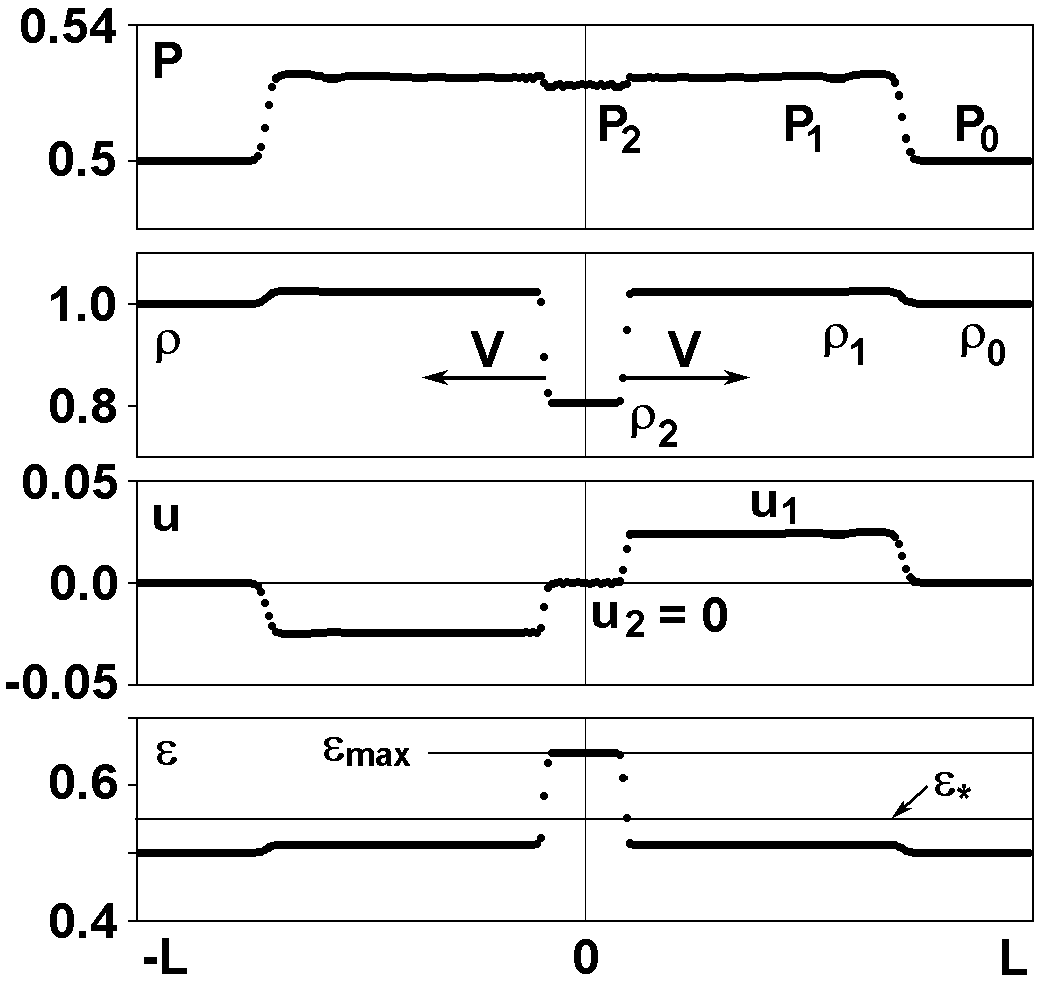
Figure 1. Structure of the selfsimilar solution. Results of
simulation with the LBE method. P is the pressure,
r is
the density, u is the mass velocity,
e is the average
kinetic energy per one particle ("temperature").
Flow Structure during Expansion of the Streamer
Conductive Channel
For the one-dimensional problem of the conductive channel
expansion a selfsimilar solution exists when three conditions are
satisfied:
1) The power released in the channel is W = const.
2) The heat conductivity inside the channel is sufficiently high,
and one can roughly consider that the energy released is
completely transferred to the channel boundary by both the
conductive heat flux and radiation.
3) The total heat flux from the channel is completely absorbed in
a thin layer of liquid. It causes a transition of the liquid
substance to the channel plasma. Under these conditions, the mass
velocity of "plasma" inside the channel is zero, and the
temperarure, density and pressure are constant both across the
channel section and in time.
Figure 1 shows flow structure for this selfsimilar solution. It
was obtained in simulation using the LBE method. In cylindrical
geometry a selfsimilar solution also exists [12], but for
W(t) = kt.
In the transition layer liquid--"plasma", a new conductive phase
is formed. This transition occurs through the flux of liquid
molecules which enter the channel plasma after their dissociation
and partial ionization. At the channel stage of discharge, the
magnitude of the flux of molecules into the channel can achieve
values much greater than
j ~
2·1024sec-1·cm-2[13].
At the initial stage of streamer propagation, the temperature inside
the conductive channel (~ 3000 K) is
rather low [14]; therefore, the density here is not much different
from the liquid density. Thus, the interface between the conductive
channel and the surrounding liquid cannot be considered as an impenetrable
piston. If the thickness of the transition layer is much less than
the channel radius, the transition layer can be treated as a
quasi-stationary gas-dynamic rupture. In the frame of reference
fixed upon the layer, the mass and momentum conservation laws take
the form
r1 D =
r2 u2 ,
P1 + r1 D2 =
P2 +
r1 D u2 .
(1)
Here P is the pressure, r
is the density, u is the mass velocity of substance,
D is the liquid inflow velocity,
u2 = V - u2
is the plasma velocity relative to the
rupture,
V = u1 + D is the observed velocity of channel
expansion (see Fig. 1).
From (1) follows a small pressure jump at a rupture,
P1 = P2 +
r2 u2
(u2 - D).
The addition to the pressure
in front of the rupture is simply the reactive pressure due
to fast liquid "vaporization". In the selfsimilar case,
u2 = 0 ,
and, hence, u2= V ,
and the pressure difference is
D P = P1 - P2
= r2 V u1 ,
which agrees quantitatively
with the value obtained in computations with the LBE method (Fig. 1).
Figure 2.
Expansion of a conductive channel and formation of shock wave.
e is the average kinetic energy per one
particle ("temperature"),
r is the average density, p is
the pressure. Computation grid 400x10,000.
Simulation of the Streamer Channel Expansion
In the present work, the LBE method was used to simulate the
channel stage of an electric discharge in liquid. The energy
release took place in a thin transition layer where
e* <
e <
emax ,
which corresponds to the energy input W = const .
Here e
is the average kinetic energy per one particle
("temperature"). Results are presented in Fig. 1. The solution
obtained is selfsimilar. The computed values agree well with
theoretical calculations.
Simulations were also performed using LG method with energy
release (Fig. 2). When
e > 0.9 the substance became
conductive and energy releases at nodes. The main difference from the
selfsimilar case (Fig. 1) is the higher heat conductivity.
Therefore, a portion of energy escapes from the channel and
"pre-heats" surrounding liquid.
Figure 3.
Propagation of the streamer tip. The velocity is 2.5. Time
t=140.
Figure 4.
Propagation of the streamer tip. The velocity is 0.6. Time
t=300.
Shock Waves in the Streamer Top Propagation
The propagation of the top of a rectilinear conductive channel
between two plane electrodes was simulated by the same method.
Density distributions averaged over 10 patterns are shown in Figs.
3 and 4. The black color indicates lower densities.
The expansion of the conductive channel and the formation of
compression waves propagating with a speed close to the sound
velocity in liquid dielectric,
C =
1/$\sqrt{2}$ � 0.7,
were observed. If the
velocity of the streamer top was higher than C,
a divergent wave with an approximately conic shape was generated.
Such waves have been observed at the prebreakdown stage of the
streamer channel propagation in the experiments of [5].
Streamer Growth
In the present work, a new model was realized in which
two-dimensional flow of a dielectric liquid is simulated by the
immiscible lattice gas (ILG) method [9] and the
transition of the dielectric to a conductive phase is described by
the field fluctuation criterion (FFC) [1,2].
A triangular lattice with six directions of particle velocity was
used. In addition, up to nine rest particles can be at each node.
The hydrodynamic flow was computed taking into account the
electric pressure
eE2/
8p acting
on the interface. The Laplace equation
Dj = 0
was then solved in the region occupied by the
dielectric. The conductive phase was considered equipotential
(j = 0). When the growth criterion
E > E* + d
was satisfied for
a node adjacent to the interface, this node and its 6 neighbors
became conductive and some energy released (the pressure
increased). In a high electric field, the boundary of a conductive
phase moves under action of the electric forces. In addition, the
conductive region expands because of the higher pressure in it.
The streamer grows as a result of both hydrodynamic movement and
the breakdown of new portions of the dielectric (transition to the
conductive state).
The relative role of these two mechanisms of development of the
conductive structure can be varied by changing the ratio between
the streamer growth velocity due to breakdown and the hydrodynamic
velocity of viscous flow.
The problem was solved in the rectangular region between two
horizontal plane electrodes to which an electric potential
difference
j(t) was applied.
Periodic boundary conditions in the X direction were used.
A transition between two mechanisms of development of the
conductive structure was demonstrated. Figure 5 shows an example
of the growth of a branched structure mainly through the breakdown
of new portions of dielectric. The structure development mainly
due to the hydrodynamic flow is presented in Fig. 6. The
bubble-like conductive region is accelerated by the electrodynamic
force. At a later stage, a flow in the form of a plane vortical
dipole moving to the upper electrode is clearly observed. The
development of conductive structures of this type has been
observed in experiments on breakdown of highly viscous dielectrics
[6] and in certain regimes of partial breakdown [7].

Figure 5.
Example of formation of branched streamer structure. t = 40.
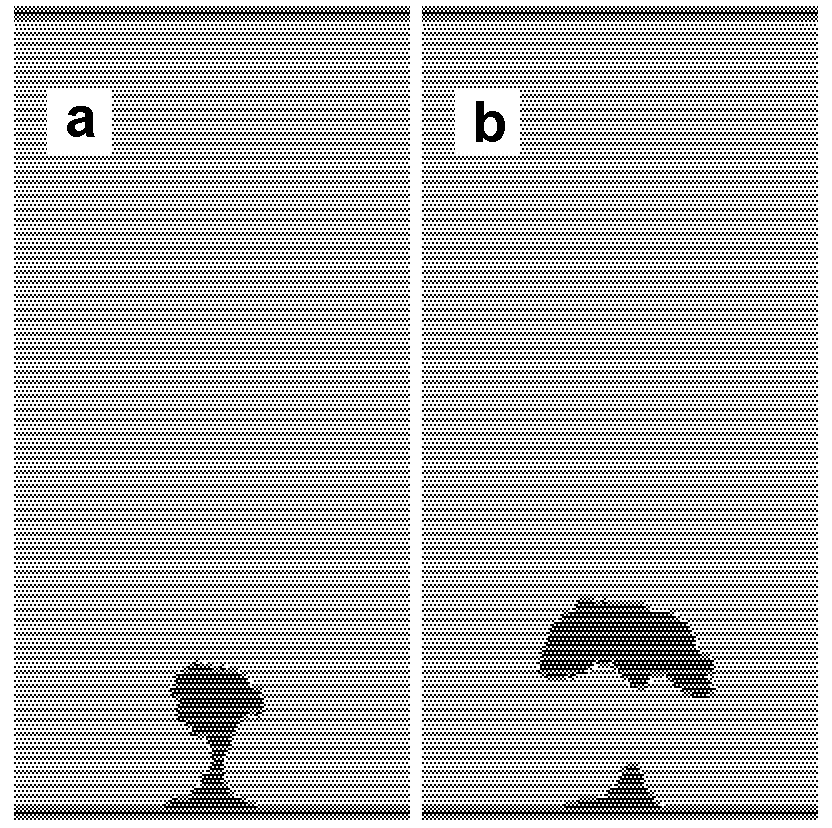
Figure 6.
Example of bubble-like streamer. Formation of a vortex. t = 200
(a) and 350 (b).
Conclusion
The gas-dynamic processes are shown to have a determinative effect
on the dynamics of the streamer structure development. One should
take them into account in constructing stochastic models of
breakdown in dielectric liquids.
Acknowledgements
This work was supported by Russian Foundation for Basic Research
under grant No. 97-02-18416.
References
- A. L. Kupershtokh,
"Fluctuation model of the breakdown of liquid
dielectrics",
Sov. Tech. Phys. Lett., Vol. 18, No. 10, pp. 647--649, 1992.
- A. P. Ershov, A. L. Kupershtokh,
"Fluctuation Model of Liquid Dielectric Breakdown with Incomplete
Charge Relaxation", in: Proc. of the 11th Int. Conf. on Conduction
and Breakdown in Dielectric Liquids, IEEE No. 93CH3204--5,
Baden-Dättwil, Switzerland, pp. 194--198, 1993.
- P. Biller, "Fractal streamer models with physical time", in:
Proc. of the 11th Int. Conf. on Conduction and Breakdown in
Dielectric Liquids, IEEE No. 93CH3204--5, Baden-Dättwil,
Switzerland, pp. 199--203, 1993.
- A. L. Kupershtokh, "Propagation of streamer top between
electrodes for fluctuation model of liquid dielectric breakdown",
in: Proc. of the 12th Int. Conf. on Conduction and Breakdown in
Dielectric Liquids, IEEE No. 96CH35981, Roma, Italy, pp. 210--213,
1996.
- P. Gournay, O. Lesaint, "Study of the dynamics of gaseous positive
streamer filaments in pentane", in: Proc. of the 11th Int. Conf.
on Conduction and Breakdown in Dielectric Liquids,
IEEE No. 93CH3204-5, Baden-Dättwil, Switzerland, pp. 289--293,
1993.
- P. K. Watson, W. G. Chadband, M. Sadeghzadeh-Araghi, "The role of
electrostatic and hydrodynamic forces in the negative-point
breakdown of liquid dielectrics", IEEE Trans. Elec. Insul.,
Vol. 26, No. 4, pp. 543--559, 1991.
- H. Yamashita, K. Yamazawa, W. Machidori, Y. S. Wang, "The effect
of tip curvature on the prebreakdown density change streamer in
cyclo-hexane", in: Proc. of the 12th Int. Conf. on Conduction and
Breakdown in Dielectric Liquids, IEEE No. 96CH35981, Roma, Italy,
pp. 226--229, 1996.
- U. Frisch, B. Hasslacher, Y. Pomeau, "Lattice-Gas automata for the
Navier-Stokes equation", Phys. Rev. Lett., Vol. 56, No. 14,
pp. 1505--1508, 1986.
- A. L. Kupershtokh, S. M. Ishchenko, A. P. Ershov, "Instability of
interface between conductive liquid and non-conductive one in
electric field", in: Proc. of the 12th Int. Conf. on Conduction
and Breakdown in Dielectric Liquids, IEEE No. 96CH35981, Roma,
Italy, pp. 107--110, 1996.
- P. Bhatnagar, E. P. Gross, M. K. Krook, "A model for collision
process in gases. I. Small amplitude process in charged and
neutral one-component system", Phys. Rev., Vol. 94. p. 511, 1954.
- Y. H. Qian, "Simulating thermohydrodynamics with lattice BGK
models", J. Sci. Comp., Vol. 8, No. 3, pp. 231--242, 1993.
- V. V. Arsent'ev, "On the theory of pulse discharge in a liquid",
J. Appl. Mech. Tech. Phys., No. 5, pp. 34--37, 1965.
- A. L. Kupershtokh, "Investigation of non-ideal plasma generated in
the channel of electric discharge in water", in: Proc. of the
15th Int. Conf. on Phenomena in Ionized Gases, Minsk, USSR,
pp. 345--346, 1981.
- P. Bårmann, S. Kröll, A. Sunesson, "Spatially and
temporally resolved electron density measurements in streamers in
dielectric liquids", J. Phys. D: Appl. Phys., Vol. 30,
pp. 856--863, 1997.
Note: To see any math constructions perfectly, run the
file through TeX; currently the WWW browsers are still not up to par
for math notations and various letter accents.
Back to Laboratory Home Page
or to A.L.Kupershtokh