 Рис.
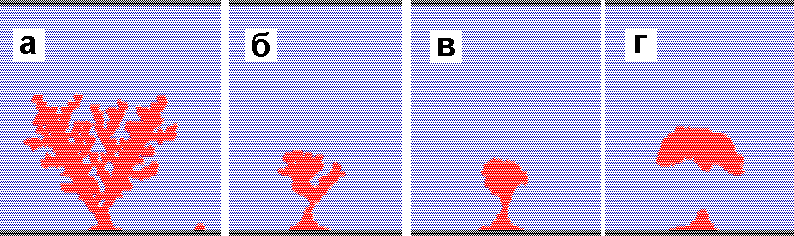
1. Форма проводящей области: a – ветвистая
стримерная структура, t = 40; в, г –
пузыреподобный стример,
формирование вихря, в – t
= 200; г
– t = 350; б
– промежуточный случай t =
210.
Рис.
1. Форма проводящей области: a – ветвистая
стримерная структура, t = 40; в, г –
пузыреподобный стример,
формирование вихря, в – t
= 200; г
– t = 350; б
– промежуточный случай t =
210. XVI Международная школа-семинар по численным методам механики вязкой жидкости
МОДЕЛИРОВАНИЕ СТОХАСТИЧЕСКОГО РОСТА СТРИМЕРОВ
С УЧЕТОМ ВЯЗКОГО ТЕЧЕНИЯ ЖИДКОГО ДИЭЛЕКТРИКА
А. Л. Куперштох
Институт гидродинамики СО РАН, Новосибирск, РОССИЯ
Многочисленные экспериментальные данные указывают на важную роль стохастических процессов при пробое жидких диэлектриков. В последние годы в их моделировании достигнуты определенные успехи [1-4]. С другой стороны, газодинамическим течениям жидкого диэлектрика при развитии пробоя до сих пор не уделялось должного внимания. Ряд экспериментов указывает на определяющую роль течений жидкости (в том числе и вихревых) при увеличении вязкости диэлектрика. При этом мелкая структура стримеров (тонких плазменных каналов) исчезает, и их развитие больше похоже на развитие полости (пузыря) неправильной формы [5]. Однако до сих пор нет модели пробоя, которая бы позволила описать (смоделировать) всю совокупность основных наблюдаемых в экспериментах явлений.
В данной работе реализована модель, в которой двумерное течение жидкого диэлектрика описывается методом несмешиваемых решеточных газов (ILG) [6], а переход вещества в проводящую фазу – флуктуационным критерием (FFC) роста стримеров [1-4].
Описание метода
Метод решеточных газов [7] рассматривает течение жидкости как динамику специальных частиц единичной массы, которые могут перелетать вдоль ребер в соседние узлы фиксированной решетки и испытывать между собой в узлах соударения и рассеяние с учетом законов сохранения. Средние во времени и пространстве величины удовлетворяют уравнению типа Навье – Стокса. Метод решеточных газов в каком-то смысле – предельно упрощенный метод молекулярной динамики. Достоинством является стохастическая природа метода.
В методе ILG существует два типа (цвета) частиц, один для жидкого диэлектрика, другой для проводящей фазы. Для подавления перемешивания жидкостей правила соударения выбираются так, чтобы поток частиц данного типа в соседние узлы, содержащие преимущественно частицы того же типа был максимален. Так моделируется поверхностное натяжение. Использовалась треугольная решетка, в узлах которой могло быть 6 частиц с разными направлениями скоростей и до 9 покоящихся частиц.
Задача решалась в прямоугольной области между двумя плоскими горизонтальными электродами, на которые подавался импульс напряжения U(t). В направлении x принимались периодические граничные условия. Гидродинамическое течение рассчитывалось с учетом действия на границе раздела фаз электрического давления ?E2/8? . ?а каждом шаге по времени в области, занятой диэлектриком, решалось уравнение Лапласа ?? = 0 ?етодом установления, модифицированным для треугольной сетки. Проводящая структура считалась эквипотенциальной ? = 0. Образование новых порций проводящей фазы на границе раздела диэлектрик–"плазма" моделировалось критерием роста стримеров (FFC). Если для узла непосредственно у границы раздела фаз E > E* + ? , ?? данный узел + 6 соседних переходят в проводящее состояние с выделением некоторой энергии (повышенное давление).
Результаты расчетов
Выполнены расчеты стохастического развития стримерной структуры с учетом газодинамических течений. В сильном электрическом поле граница проводящей фазы двигается под действием электродинамических сил и, кроме того, проводящая область расширяется за счет повышенного в ней давления. В итоге рост стримера происходит как за счет гидродинамического движения области проводящей фазы, так и за счет пробоя новых порций диэлектрика (переход их в проводящее состояние). Относительную роль этих двух механизмов развития проводящей структуры можно варьировать путем изменения соотношения между скоростью роста стримера за счет пробоя и гидродинамической скоростью вязкого течения.
На рис. 1,а показан пример развития ветвистой стримерной структуры в основном по механизму пробоя новых порций диэлектрика. Рост структуры главным образом за счет гидродинамического течения показан на рис. 1,в-г. Проводящая область пузыреподобной формы ускоряется электродинамической силой. При этом на поздних стадиях четко наблюдается течение в виде плоского вихревого диполя, поднимающегося к верхнему электроду. Развитие процесса по такому сценарию наблюдалось в экспериментах при пробое сильно вязких диэлектриков [5] и при определенных режимах частичного пробоя [8]. На рис. 1,б представлен промежуточный вариант.
Показано, что газодинамические течения оказывают определяющее влияние на динамику развития стримерных структур, и их необходимо учитывать при построении моделей пробоя жидких диэлектриков. Работа выполнена при поддержке РФФИ (грант 97-02-18416).
 Рис.
1. Форма проводящей области: a – ветвистая
стримерная структура, t = 40; в, г –
пузыреподобный стример,
формирование вихря, в – t
= 200; г
– t = 350; б
– промежуточный случай t =
210.
Рис.
1. Форма проводящей области: a – ветвистая
стримерная структура, t = 40; в, г –
пузыреподобный стример,
формирование вихря, в – t
= 200; г
– t = 350; б
– промежуточный случай t =
210.